numericalderivative documentation¶
numericalderivative is a module for numerical differentiation.
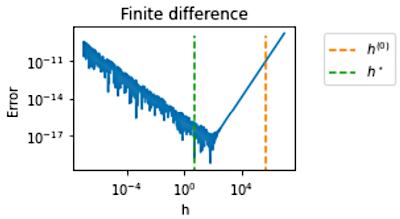
The goal of this project is to compute the derivative of a function using finite difference formulas. The difficulty with these formulas is that it must use a step which must be neither too large (otherwise the truncation error dominates the error) nor too small (otherwise the condition error dominates). For this purpose, it provides exact methods (based on the value of higher derivatives) and approximate methods (based on function values). Furthermore, the module provides finite difference formulas for the first, second, third or any arbitrary order derivative of a function. Finally, this package provides 15 benchmark problems for numerical differentiation.
Documentation about numericalderivative can be found here
User documentation¶
- User manual
- Algorithms for optimal step
- Finite Differences
- numericalderivative.FunctionWithArguments
- numericalderivative.FiniteDifferenceFormula
- numericalderivative.FirstDerivativeForward
- numericalderivative.FirstDerivativeCentral
- numericalderivative.SecondDerivativeCentral
- numericalderivative.ThirdDerivativeCentral
- numericalderivative.GeneralFiniteDifference
- Benchmark problems
- numericalderivative.DerivativeBenchmarkProblem
- numericalderivative.PolynomialProblem
- numericalderivative.InverseProblem
- numericalderivative.ExponentialProblem
- numericalderivative.LogarithmicProblem
- numericalderivative.SquareRootProblem
- numericalderivative.AtanProblem
- numericalderivative.SinProblem
- numericalderivative.ScaledExponentialProblem
- numericalderivative.GMSWExponentialProblem
- numericalderivative.SXXNProblem1
- numericalderivative.SXXNProblem2
- numericalderivative.SXXNProblem3
- numericalderivative.SXXNProblem4
- numericalderivative.OliverProblem1
- numericalderivative.OliverProblem2
- numericalderivative.OliverProblem3
- Benchmark features
Examples¶
- Examples
- A simple demonstration of the methods
- Applies Stepleman & Winarsky method to an OpenTURNS function
- Use the benchmark problems
- Use the finite differences formulas
- Use the generalized finite differences formulas
- Convergence of the generalized finite differences formulas
- Dumontet & Vignes
- Gill, Murray, Saunders & Wright
- Stepleman & Winarsky
- Shi, Xie, Xuan & Nocedal
References¶
Gill, P. E., Murray, W., Saunders, M. A., & Wright, M. H. (1983). Computing forward-difference intervals for numerical optimization. SIAM Journal on Scientific and Statistical Computing, 4(2), 310-321.
Adaptive numerical differentiation. R. S. Stepleman and N. D. Winarsky. Journal: Math. Comp. 33 (1979), 1257-1264
Dumontet, J., & Vignes, J. (1977). Détermination du pas optimal dans le calcul des dérivées sur ordinateur. RAIRO. Analyse numérique, 11 (1), 13-25.