Note
Go to the end to download the full example code.
Experiment with Shi, Xie, Xuan & Nocedal general method¶
Find a step which is near to optimal for a general finite difference formula.
References¶
Shi, H. J. M., Xie, Y., Xuan, M. Q., & Nocedal, J. (2022). Adaptive finite-difference interval estimation for noisy derivative-free optimization. SIAM Journal on Scientific Computing, 44 (4), A2302-A2321.
import numpy as np
import pylab as pl
import numericalderivative as nd
from matplotlib.ticker import MaxNLocator
Use the method on a simple problem¶
In the next example, we use the algorithm on the exponential function.
We create the ShiXieXuanNocedalGeneral algorithm using the function and the point x.
Then we use the find_step() method to compute the step,
using an upper bound of the step as an initial point of the algorithm.
Finally, use the compute_first_derivative() method to compute
an approximate value of the first derivative using finite differences.
The get_number_of_function_evaluations() method
can be used to get the number of function evaluations.
x = 1.0
differentiation_order = 1 # First derivative
formula_accuracy = 2 # Order 2
formula = nd.GeneralFiniteDifference(
np.exp,
x,
differentiation_order,
formula_accuracy,
direction="central", # Central formula
)
algorithm = nd.ShiXieXuanNocedalGeneral(formula, verbose=True)
initial_step = 1.0
step, number_of_iterations = algorithm.find_step(initial_step)
f_prime_approx = algorithm.compute_derivative(step)
feval = algorithm.get_number_of_function_evaluations()
f_prime_exact = np.exp(x) # Since the derivative of exp is exp.
print(f"Computed step = {step:.3e}")
print(f"Number of iterations = {number_of_iterations}")
print(f"f_prime_approx = {f_prime_approx}")
print(f"f_prime_exact = {f_prime_exact}")
absolute_error = abs(f_prime_approx - f_prime_exact)
x = 1.0
absolute_precision = 1.000e-15
estim_step=1.000e+00
+ Iter.=0, lower_bound=0.000e+00, upper_bound=inf, estim_step=1.000e+00, r = 1.735e+15
- test_ratio > self.minimum_test_ratio. Set upper bound to h.
- lower_bound == 0: decrease h.
+ Iter.=1, lower_bound=0.000e+00, upper_bound=1.000e+00, estim_step=2.500e-01, r = 2.157e+13
- test_ratio > self.minimum_test_ratio. Set upper bound to h.
- lower_bound == 0: decrease h.
+ Iter.=2, lower_bound=0.000e+00, upper_bound=2.500e-01, estim_step=6.250e-02, r = 3.321e+11
- test_ratio > self.minimum_test_ratio. Set upper bound to h.
- lower_bound == 0: decrease h.
+ Iter.=3, lower_bound=0.000e+00, upper_bound=6.250e-02, estim_step=1.562e-02, r = 5.185e+09
- test_ratio > self.minimum_test_ratio. Set upper bound to h.
- lower_bound == 0: decrease h.
+ Iter.=4, lower_bound=0.000e+00, upper_bound=1.562e-02, estim_step=3.906e-03, r = 8.101e+07
- test_ratio > self.minimum_test_ratio. Set upper bound to h.
- lower_bound == 0: decrease h.
+ Iter.=5, lower_bound=0.000e+00, upper_bound=3.906e-03, estim_step=9.766e-04, r = 1.266e+06
- test_ratio > self.minimum_test_ratio. Set upper bound to h.
- lower_bound == 0: decrease h.
+ Iter.=6, lower_bound=0.000e+00, upper_bound=9.766e-04, estim_step=2.441e-04, r = 1.978e+04
- test_ratio > self.minimum_test_ratio. Set upper bound to h.
- lower_bound == 0: decrease h.
+ Iter.=7, lower_bound=0.000e+00, upper_bound=2.441e-04, estim_step=6.104e-05, r = 3.090e+02
- test_ratio > self.minimum_test_ratio. Set upper bound to h.
- lower_bound == 0: decrease h.
+ Iter.=8, lower_bound=0.000e+00, upper_bound=6.104e-05, estim_step=1.526e-05, r = 4.774e+00
- Step = 1.52587890625e-05 is OK: stop.
Computed step = 1.526e-05
Number of iterations = 8
f_prime_approx = 2.718281828565523
f_prime_exact = 2.718281828459045
Use the method on the ScaledExponentialProblem¶
Consider this problem.
problem = nd.ScaledExponentialProblem()
print(problem)
name = problem.get_name()
x = problem.get_x()
third_derivative = problem.get_third_derivative()
third_derivative_value = third_derivative(x)
optimum_step, absolute_error = nd.FirstDerivativeCentral.compute_step(
third_derivative_value
)
print(f"Name = {name}, x = {x}")
print(f"Optimal step for central finite difference formula = {optimum_step}")
print(f"Minimum absolute error= {absolute_error}")
DerivativeBenchmarkProblem
name = scaled exp
x = 1.0
f(x) = 0.9999990000005
f'(x) = -9.999990000004999e-07
f''(x) = 9.999990000005e-13
f^(3)(x) = -9.999990000005e-19
f^(4)(x) = 9.999990000004998e-25
f^(5)(x) = -9.999990000004998e-31
Name = scaled exp, x = 1.0
Optimal step for central finite difference formula = 6.694331732265233
Minimum absolute error= 2.2407016263779204e-17
Plot the error vs h¶
function = problem.get_function()
first_derivative = problem.get_first_derivative()
finite_difference = nd.FirstDerivativeCentral(function, x)
number_of_points = 1000
step_array = np.logspace(-8.0, 4.0, number_of_points)
error_array = np.zeros((number_of_points))
for i in range(number_of_points):
h = step_array[i]
f_prime_approx = finite_difference.compute(h)
error_array[i] = abs(f_prime_approx - first_derivative(x))
pl.figure()
pl.plot(step_array, error_array)
pl.plot([optimum_step] * 2, [min(error_array), max(error_array)], label=r"$h^*$")
pl.title("Central finite difference")
pl.xlabel("h")
pl.ylabel("Error")
pl.xscale("log")
pl.yscale("log")
pl.legend(bbox_to_anchor=(1, 1))
pl.tight_layout()
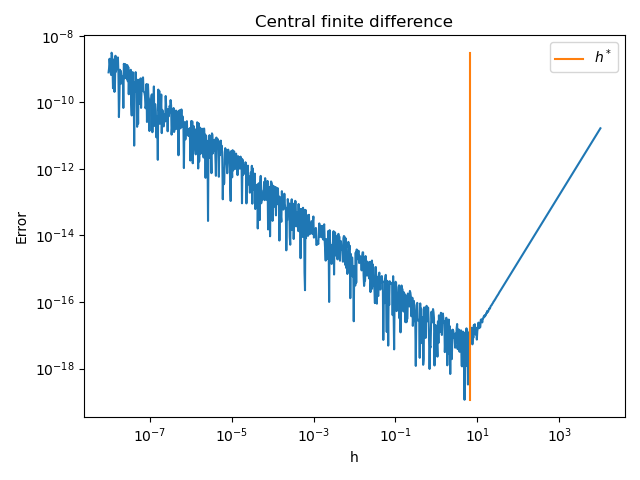
Use the algorithm to detect h*
differentiation_order = 1
formula_accuracy = 2
formula = nd.GeneralFiniteDifference(
function,
x,
differentiation_order,
formula_accuracy,
direction="central", # Central formula
)
algorithm = nd.ShiXieXuanNocedalGeneral(formula, verbose=True)
x = 1.0e0
initial_step = 1.0
h_optimal, iterations = algorithm.find_step(initial_step)
number_of_function_evaluations = algorithm.get_number_of_function_evaluations()
print("Optimum h =", h_optimal)
print("iterations =", iterations)
print("Function evaluations =", number_of_function_evaluations)
f_prime_approx = algorithm.compute_derivative(h_optimal)
absolute_error = abs(f_prime_approx - problem.first_derivative(x))
print("Error = ", absolute_error)
x = 1.0
absolute_precision = 1.000e-15
estim_step=1.000e+00
+ Iter.=0, lower_bound=0.000e+00, upper_bound=inf, estim_step=1.000e+00, r = 0.000e+00
- test_ratio < self.minimum_test_ratio. Set lower bound to h.
- upper_bound == np.inf: increase h.
+ Iter.=1, lower_bound=1.000e+00, upper_bound=inf, estim_step=4.000e+00, r = 5.551e-02
- test_ratio < self.minimum_test_ratio. Set lower bound to h.
- upper_bound == np.inf: increase h.
+ Iter.=2, lower_bound=4.000e+00, upper_bound=inf, estim_step=1.600e+01, r = 1.998e+00
- Step = 16.0 is OK: stop.
Optimum h = 16.0
iterations = 2
Function evaluations = 18
Error = 4.34386023922791e-17
Plot the criterion depending on the step¶
Plot the test ratio depending on h
problem = nd.ScaledExponentialProblem()
function = problem.get_function()
name = problem.get_name()
x = problem.get_x()
differentiation_order = 1
formula_accuracy = 2
formula = nd.GeneralFiniteDifference(
function,
x,
differentiation_order,
formula_accuracy,
direction="central", # Central formula
)
algorithm = nd.ShiXieXuanNocedalGeneral(formula, verbose=True)
minimum_test_ratio, maximum_test_ratio = algorithm.get_ratio_min_max()
absolute_precision = 1.0e-15
number_of_points = 500
step_array = np.logspace(-10.0, 3.0, number_of_points)
test_ratio_array = np.zeros((number_of_points))
for i in range(number_of_points):
test_ratio_array[i] = algorithm.compute_test_ratio(
step_array[i],
)
pl.figure()
pl.plot(step_array, test_ratio_array, "-", label="Test ratio")
pl.plot(step_array, [minimum_test_ratio] * number_of_points, "--", label="Min")
pl.plot(step_array, [maximum_test_ratio] * number_of_points, ":", label="Max")
pl.title(f"{name} at x = {x}. Test ratio.")
pl.xlabel("h")
pl.ylabel(r"$r$")
pl.xscale("log")
pl.yscale("log")
pl.legend()
pl.tight_layout()

See the history of steps during the search¶
In Shi, Xie, Xuan & Nocedal's method, the algorithm
produces a sequence of steps \((h_i)_{1 \leq i \leq n_{iter}}\)
where \(n_{iter} \in \mathbb{N}\) is the number of iterations.
These steps are meant to converge to an
approximately optimal step of for the finite difference formula of the
derivative.
The optimal step \(h^\star\) for the finite difference formula of the
derivative can be computed depending on some derivative of the
function.
In the next example, we want to compute the absolute error between
each intermediate step \(h_i\) and the exact value \(h^\star\)
to see how close the algorithm gets to the exact step.
The list of intermediate steps during the algorithm can be obtained
thanks to the get_step_history() method.
In the next example, we print the intermediate steps k during the bissection algorithm that searches for a step such that the L ratio is satisfactory.
problem = nd.ScaledExponentialProblem()
function = problem.get_function()
name = problem.get_name()
x = problem.get_x()
differentiation_order = 1
formula_accuracy = 2
formula = nd.GeneralFiniteDifference(
function,
x,
differentiation_order,
formula_accuracy,
direction="central", # Central formula
)
algorithm = nd.ShiXieXuanNocedalGeneral(formula, verbose=True)
initial_step = 1.0e5
step, number_of_iterations = algorithm.find_step(initial_step)
step_h_history = algorithm.get_step_history()
print(f"Number of iterations = {number_of_iterations}")
print(f"History of steps h : {step_h_history}")
last_step_h = step_h_history[-1]
print(f"Last step h : {last_step_h}")
x = 1.0
absolute_precision = 1.000e-15
estim_step=1.000e+05
+ Iter.=0, lower_bound=0.000e+00, upper_bound=inf, estim_step=1.000e+05, r = 5.013e+11
- test_ratio > self.minimum_test_ratio. Set upper bound to h.
- lower_bound == 0: decrease h.
+ Iter.=1, lower_bound=0.000e+00, upper_bound=1.000e+05, estim_step=2.500e+04, r = 7.814e+09
- test_ratio > self.minimum_test_ratio. Set upper bound to h.
- lower_bound == 0: decrease h.
+ Iter.=2, lower_bound=0.000e+00, upper_bound=2.500e+04, estim_step=6.250e+03, r = 1.221e+08
- test_ratio > self.minimum_test_ratio. Set upper bound to h.
- lower_bound == 0: decrease h.
+ Iter.=3, lower_bound=0.000e+00, upper_bound=6.250e+03, estim_step=1.562e+03, r = 1.907e+06
- test_ratio > self.minimum_test_ratio. Set upper bound to h.
- lower_bound == 0: decrease h.
+ Iter.=4, lower_bound=0.000e+00, upper_bound=1.562e+03, estim_step=3.906e+02, r = 2.980e+04
- test_ratio > self.minimum_test_ratio. Set upper bound to h.
- lower_bound == 0: decrease h.
+ Iter.=5, lower_bound=0.000e+00, upper_bound=3.906e+02, estim_step=9.766e+01, r = 4.657e+02
- test_ratio > self.minimum_test_ratio. Set upper bound to h.
- lower_bound == 0: decrease h.
+ Iter.=6, lower_bound=0.000e+00, upper_bound=9.766e+01, estim_step=2.441e+01, r = 7.272e+00
- test_ratio > self.minimum_test_ratio. Set upper bound to h.
- lower_bound == 0: decrease h.
+ Iter.=7, lower_bound=0.000e+00, upper_bound=2.441e+01, estim_step=6.104e+00, r = 1.110e-01
- test_ratio < self.minimum_test_ratio. Set lower bound to h.
- Bisection: estim_step = 1.221e+01.
+ Iter.=8, lower_bound=6.104e+00, upper_bound=2.441e+01, estim_step=1.221e+01, r = 9.437e-01
- test_ratio < self.minimum_test_ratio. Set lower bound to h.
- Bisection: estim_step = 1.726e+01.
+ Iter.=9, lower_bound=1.221e+01, upper_bound=2.441e+01, estim_step=1.726e+01, r = 2.665e+00
- Step = 17.263349150062194 is OK: stop.
Number of iterations = 9
History of steps h : [100000.0, 25000.0, 6250.0, 1562.5, 390.625, 97.65625, 24.4140625, 6.103515625, np.float64(12.20703125), np.float64(17.263349150062194)]
Last step h : 17.263349150062194
Then we compute the exact step, using compute_step().
third_derivative = problem.get_third_derivative()
third_derivative_value = third_derivative(x)
print(f"f^(3)(x) = {third_derivative_value}")
absolute_precision = 1.0e-16
exact_step, absolute_error = nd.FirstDerivativeCentral.compute_step(
third_derivative_value, absolute_precision
)
print(f"Optimal step k for f'(x) using forward F.D. = {exact_step}")
f^(3)(x) = -9.999990000005e-19
Optimal step k for f'(x) using forward F.D. = 6.694331732265233
Plot the absolute error between the exact step k and the intermediate k of the algorithm.
error_step_h = [abs(step_h_history[i] - exact_step) for i in range(len(step_h_history))]
fig = pl.figure(figsize=(4.0, 3.0))
pl.title(f"Shi, Xie, Xuan & Nocedal on {name} at x = {x}")
pl.plot(range(len(step_h_history)), error_step_h, "o-")
pl.xlabel("Iterations")
pl.ylabel(r"$|h_i - h^\star|$")
pl.yscale("log")
ax = fig.gca()
ax.xaxis.set_major_locator(MaxNLocator(integer=True))
pl.tight_layout()
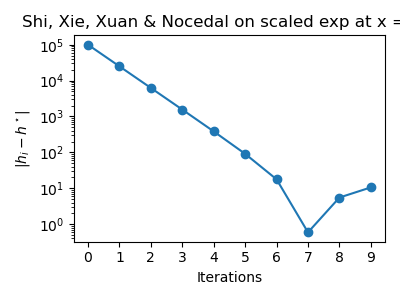
The previous figure shows that the algorithm converges relatively fast. The absolute error does not evolve monotically.
Total running time of the script: (0 minutes 0.644 seconds)